快速排序算法的介绍
1. 简介
在本教程中,我们将研究快速排序算法并了解它是如何工作的。
快速排序是一种分而治之的算法。这意味着每次迭代的工作原理是将输入分成两部分,然后对它们进行排序,然后再将它们组合在一起
它最初由 Tony Hoare 开发并于 1961 年发布,它仍然是可用的更有效的通用排序算法之一。
2. 算法要求
使用快速排序算法的唯一真正要求是比较两个元素的定义明确的操作。我们可以确定任何元素是否严格小于另一个元素。这种比较的确切性质并不重要,只要它是一致的。请注意,不需要直接相等比较,只需要小于比较。
对于许多类型,这是一个不可否认的比较。例如,数字隐含地定义了如何执行此操作。其他类型不太明显,但我们仍然可以根据排序的要求来定义它。例如,在对字符串进行排序时,我们需要确定字符大小写是否重要或 Unicode 字符如何工作。
3. 二叉树排序
二叉树排序是一种算法,我们在其中构建由我们正在排序的元素组成的平衡二叉树。一旦我们有了这个,我们就可以从这棵树中构建结果。
这个想法是选择一个Pivot作为树上的节点,然后 根据它们是否小于枢轴元素,将所有元素分配给节点的Left分支或 Right分支。然后我们可以递归地对这些分支进行排序,直到我们有一个完全排序的树。
3.1. 工作示例
例如,要对数字列表“3 7 8 5 2 1 9 5 4”进行排序,我们的第一遍将如下所示:
Input: 3 7 8 5 2 1 9 5 4
Pivot = 3
Left = 2 1
Right = 7 8 5 9 5 4
这给了我们原始输入的两个分区。Left列表中的所有内容都严格小于 Pivot,而其他所有内容都在Right列表中**。
接下来,我们使用相同的算法对这两个列表进行排序:
Input: 2 1
Pivot = 2
Left = 1
Right = Empty
Input: 7 8 5 9 5 4
Pivot = 7
Left = 5 5 4
Right = 8 9
当我们从第一遍对左侧分区进行排序时,我们最终得到了两个长度为 1 或更少的列表。然后这些已经排序——因为不可能有一个未排序的大小为 1 的列表。这意味着我们可以在这里停下来,而是专注于正确分区的剩余部分。
此时,我们有以下结构:
/ [1]
2
/ \ []
3
\ / [5 5 4]
7
\ [8 9]
我们可以看到我们已经接近排序列表了。我们还有两个分区要排序,然后我们就完成了:
1
/
2 4
/ /
3 5
\ / \
7 5
\
8
\
9
这在算法的 5 遍中对列表进行了排序,适用于越来越小的子列表。但是,内存需求相对较高,必须额外分配 17 个元素的内存来对原始列表中的 9 个元素进行排序。
4. 快速排序的总体思路
快速排序算法在概念上类似于二叉树排序。它不是在我们需要排序的每个步骤中构建子列表,而是在原始列表中完成所有工作。
它的工作原理是围绕选定的枢轴动态交换列表中的元素,然后递归地将子列表排序到该枢轴的任一侧。这使得它的空间效率显着提高,这对于大型列表可能很重要。
快速排序取决于两个关键因素——选择主*pivot *和 *partitioning *元素的机制。
**这个算法的关键是 partition 函数,我们很快就会讲到。这将返回输入数组的索引,使得该索引下方的每个元素排序为小于该索引处的元素,并且该索引处的元素排序为小于其上方的所有元素。
这样做将涉及交换数组中的一些元素,以使它们成为该索引的适当一侧。
一旦我们完成了这个分区,我们就将算法应用到这个索引两侧的两个分区上。当我们的分区每个只包含一个元素时,这最终完成,此时输入数组现在已排序。
因此,我们可以将快速排序算法总结为三个步骤:
- 选择一个元素作为枢轴
- 通过将较小的元素移动到枢轴的左侧并将较大的元素移动到其右侧来划分问题集
- 在每个分区上重复上述步骤
5. 快速排序示例
这里我们有一个包含十个未排序值的数组,我们将使用 Quicksort 对其进行排序:
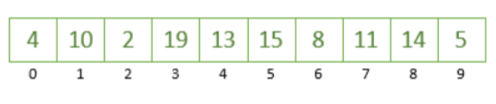
**我们要采取的第一步是从这个数组中选择一个元素作为我们的枢轴。**我们可以用不同的方式选择一个主元,但对于这个例子,我们总是选择数组的最右边的元素,即数字 5。
现在我们已经确定了 5 作为我们的枢轴,让我们根据我们的枢轴对数组进行分区,将大于 5 的数字放在右侧,将小于 5 的数字放在左侧。在这一点上,我们并不真正担心对数字进行排序,只是我们已经将它们移动到关于枢轴的正确位置。
在此过程中,我们将数组围绕枢轴 5 划分为两部分:

让我们取最左边的分区(索引 0 - 1)并重复这些步骤。我们将选择数字 2 作为我们的支点并相应地重新排列,这为我们提供了以下信息:

接下来,我们取最右边的分区(索引 3 - 9)并将 10 作为我们的枢轴;任何大于 10 的数字都将移至其右侧,小于 10 的数字将移至其左侧:

正如我们通过定位每个选定的枢轴所看到的那样,我们正在慢慢接近排序数组!如果我们继续在索引 5 到 9 的剩余分区上重复这些步骤,我们将最终达到我们的数组从最小到最大排序的点。
下图显示了所有步骤,最终为我们提供了一个排序数组:
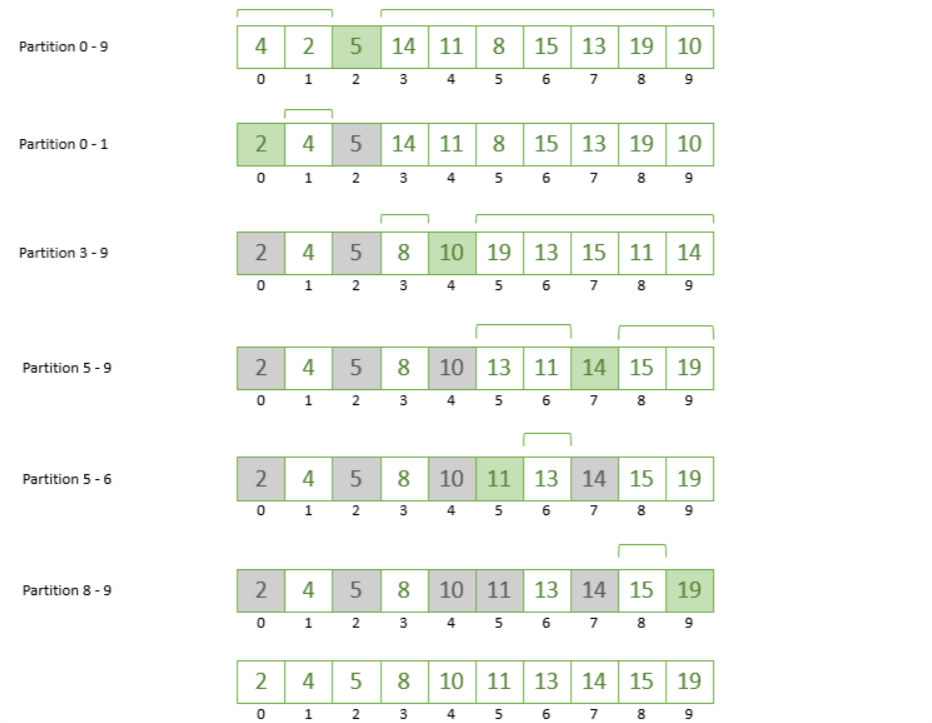
正如我们所看到的,这些步骤可能会根据我们选择枢轴元素的方式而有所不同。因此,让我们开始讨论选择支点的主要方法。
6. 快速排序实现
快速排序算法有多种实现。这些实现在选择枢轴元素的方式方面彼此不同。让我们讨论分区方法。
6.1. Lomuto 分区
Lomuto 分区归功于 Nico Lomuto。这通过迭代输入数组来工作,交换严格小于预先选择的枢轴元素的元素。它们出现在数组的较早位置,但在滑动目标索引上。
然后,这个滑动目标索引就是我们将返回的新分区索引,以供更大算法的下一次递归使用。
这是为了确保我们的滑动目标索引的位置使得数组中它之前的所有元素都小于这个元素,并且这个元素小于数组中它之后的所有元素。
让我们用伪代码来看看这个:
fun quicksort(input : T[], low : int, high : int)
if (low < high)
p := partition(input, low, high)
quicksort(input, low, p - 1)
quicksort(input, p + 1, high)
fun partition(input: T[], low: int, high: int) : int
pivot := input[high]
partitionIndex := low
loop j from low to (high - 1)
if (input[j] < pivot) then
swap(input[partitionIndex], input[j])
partitionIndex := partitionIndex + 1
swap(input[partitionIndex], input[high]
return partitionIndex
作为一个工作示例,我们可以从之前对数组进行分区:
Sorting input: 3,7,8,5,2,1,9,5,4 from 0 to 8
Pivot: 4
Partition Index: 0
When j == 0 => input[0] == 3 => Swap 3 for 3 => input := 3,7,8,5,2,1,9,5,4, partitionIndex := 1
When j == 1 => input[1] == 7 => No Change
When j == 2 => input[2] == 8 => No Change
When j == 3 => input[3] == 5 => No Change
When j == 4 => input[4] == 7 => Swap 7 for 2 => input := 3,2,8,5,7,1,9,5,4, partitionIndex := 2
When j == 5 => input[5] == 8 => Swap 8 for 1 => input := 3,2,1,5,7,8,9,5,4, partitionIndex := 3
When j == 6 => input[6] == 9 => No Change
When j == 7 => input[7] == 5 => No Change
After Loop => Swap 4 for 5 => input := 3,2,1,4,7,8,9,5,5, partitionIndex := 3
通过这个我们可以看到,我们已经执行了 3 次交换,并确定了索引“3”的新分区点。这些交换之后的数组使得元素 0、1 和 2 都小于元素 3,并且元素 3 小于元素 4、5、6、7 和 8。
完成此操作后,将递归更大的算法,这样我们将从 0 到 2 对子数组进行排序,从 4 到 8 对子数组进行排序。例如,对从 0 到 2 的子数组重复此操作,我们会这样做:
Sorting input: 3,2,1,4,7,8,9,5,5 from 0 to 2
Pivot: 1
Partition Index: 0
When j == 0 => input[0] == 3 => No Change
When j == 1 => input[1] == 2 => No Change
After Loop => Swap 1 for 3 => input := 1,2,3,4,7,8,9,5,5, partitionIndex := 0
请注意,我们仍在传递整个输入数组以供算法使用,但因为我们有低和高索引,我们实际上只关注我们关心的位。这是一种效率,意味着我们不需要复制整个数组或其中的部分。
在整个算法中,对整个数组进行排序,我们执行了 12 次不同的交换以获得结果。
6.2. Hoare分区
Hoare 分区是由 Tony Hoare 在 Quicksort 算法最初发布时提出的。它不是从低到高跨数组工作,而是从两端一次向中心迭代。这意味着我们有更多的迭代,更多的比较,但更少的交换。
这可能很重要,因为通常比较内存值比交换它们便宜。
在伪代码中:
fun quicksort(input : T[], low : int, high : int)
if (low < high)
p := partition(input, low, high)
quicksort(input, low, p) // Note that this is different than when using Lomuto
quicksort(input, p + 1, high)
fun partition(input : T[], low: int, high: int) : int
pivotPoint := floor((high + low) / 2)
pivot := input[pivotPoint]
high++
low--
loop while True
low++
loop while (input[low] < pivot)
high--
loop while (input[high] > pivot)
if (low >= high)
return high
swap(input[low], input[high])
作为一个工作示例,我们可以从之前对数组进行分区:
Sorting input: 3,7,8,5,2,1,9,5,4 from 0 to 8
Pivot: 2
Loop #1
Iterate low => input[0] == 3 => Stop, low == 0
Iterate high => input[8] == 4 => high := 7
Iterate high => input[7] == 5 => high := 6
Iterate high => input[6] == 9 => high := 5
Iterate high => input[5] == 1 => Stop, high == 5
Swap 1 for 3 => input := 1,7,8,5,2,3,9,5,4
Low := 1
High := 4
Loop #2
Iterate low => input[1] == 7 => Stop, low == 1
Iterate high => input[4] == 2 => Stop, high == 4
Swap 2 for 7 => input := 1,2,8,5,7,3,9,5,4
Low := 2
High := 3
Loop #3
Iterate low => input[2] == 8 => Stop, low == 2
Iterate high => input[3] == 5 => high := 2
Iterate high => input[2] == 8 => high := 1
Iterate high => input[1] == 2 => Stop, high == 1
Return 1
从表面上看,这看起来是一个更复杂的算法,正在做更多的工作。但是,总体而言,它的工作成本较低。整个算法只需要 8 次交换而不是 Lomuto 分区方案所需的 12 次即可达到相同的结果。
7. 算法调整
根据具体要求,我们可以对正常算法进行一些调整。这些并不适合每种情况,因此我们应该仅在适当的时候使用它们,但它们可以对结果产生重大影响。
7.1. Pivot 选择
选择要围绕的元素对算法的效率具有重要意义。上面,我们选择了一个固定元素。如果列表真正按随机顺序打乱,这很有效,但列表越有序,效率就越低。
如果我们要对列表 1, 2, 3, 4, 5, 6, 7, 8, 9进行排序,那么 Hoare 分区方案以零交换进行排序,但 Lomuto 方案需要 44。同样,列表 9, 8, 7、6、5、4、3、2、1 需要与 Hoare 交换 4次,与 Lomuto 交换 24 次。
在 Hoare 分区方案中,这已经很不错了,但是 Lomuto 方案可以改进很多。通过改变我们选择枢轴的方式,通过使用三个固定点的中值,我们可以获得显着的改进。
这种调整简称为三中位数:
mid := (low + high) / 2
if (input[mid] < input[low])
swap(input[mid], input[low])
if (input[high] < input[low])
swap(input[high], input[low])
if (input[mid] < input[high])
swap(input[mid], input[high])
我们将其应用于算法的每一次通过。这需要三个固定点并确保它们以相反的顺序预先排序。
这似乎不寻常,但影响不言而喻。使用它对列表 1、2、3、4、5、6、7、8、9进行排序现在需要 16 次交换,而之前需要 44 次。这减少了 64% 的工作量。但是,列表 9, 8, 7, 6, 5, 4, 3, 2, 1只下降到 19 次交换,而不是之前的 24 次,列表 3, 7, 8, 5, 2, 1, 9 , 5, 4从之前的 12 上升到 18。
7.2. 重复元素
当有大量直接相等的元素时,快速排序会受到轻微影响。它仍然会尝试对所有这些进行排序,并且可能会做很多不必要的工作。
我们可以做的一个调整是在分割阶段检测这些相等的元素,并在它们的任一侧返回边界,而不仅仅是一个点。然后,我们可以将一整段相等的元素视为已经排序,并只处理两边的元素。
让我们用伪代码来看看:
fun quicksort(input : T[], low : int, high : int)
if (low < high)
(left, right) := partition(input, low, high)
quicksort(input, low, left - 1)
quicksort(input, right + 1, high)
每次分区方案返回一个主元时,它都会返回所有具有相同值的相邻元素的下索引和上索引。这可以快速删除列表的较大部分,而无需处理它们。
为了实现这一点,我们需要能够比较元素的相等和小于。然而,这通常是更容易实现的比较。
8. 算法性能
快速排序算法通常被认为是非常有效的。平均而言,它具有$$O(n\log(n))$$对任意输入进行排序的性能。
原始的 Lomuto 分区方案将降级为$$O(n)$$列表已经排序并且我们选择最终元素作为枢轴的情况。正如我们所见,当我们为枢轴选择实施三中位数时,这种情况会有所改善,事实上,这会将我们带回到$$O(n\log(n))$$。
相反,Hoare 分区方案可能会导致更多的比较,因为它递归 $$low \rightarrow p$$ 而不是$$low \rightarrow p-1$$ . 这意味着递归进行更多比较,即使它导致更少的交换。
 Coding Man
Coding Man