Java折叠技术简介

1. 简介

在本教程中，我们将考虑在各种数据结构中使用的散列技术，这些数据结构提供对其元素的恒定时间访问。

我们更详细地讨论了所谓的折叠技术，并简要介绍了 mid-square 和 binning 技术。

2.概述

当我们选择存储对象的数据结构时，考虑因素之一是我们是否需要快速访问它们。

Java 实用程序包为我们提供了大量用于存储对象的数据结构。有关数据结构的更多信息，请参阅我们的Java 集合 编译页面，其中包含其中几个的指南。

正如我们所知，其中一些数据结构允许我们在恒定时间内检索它们的元素，而与它们包含的元素数量无关。

可能，最简单的一个是数组。事实上，我们通过索引访问数组中的元素。**访问时间自然不取决于数组的大小。**事实上，在幕后，许多数据结构大量使用数组。

问题是数组索引必须是数字，而我们通常更喜欢用对象来操作这些数据结构。

为了解决这个问题，许多数据结构都试图为对象分配一个可以作为数组索引的数值。我们称这个值为散列值或简称为散列。

3. 散列

散列 是将对象转换为数值**。**执行这些转换的函数称为散列函数。

为了简单起见，让我们考虑将字符串转换为数组索引的哈希函数，即将转换为*[0, N]范围内具有有限N*的整数。

自然地，散列函数适用于各种各样的字符串。因此，它的“全局”属性变得很重要。

不幸的是，哈希函数不可能总是将不同的字符串转换为不同的数字。

我们可以很容易地说服自己，字符串的数量远大于*[0, N]范围内整数的数量。因此，不可避免地存在一对不相等的字符串，哈希函数为其生成相等的值。**这种现象称为碰撞*。**

我们不打算深入研究散列函数背后的工程细节，但很明显，一个好的散列函数应该尝试将定义它的字符串统一映射为数字。

另一个明显的要求是好的散列函数应该很快。如果计算哈希值的时间太长，那么我们就无法快速访问元素。

在本教程中，我们考虑了一种尝试使映射统一同时保持快速的技术。

4. 折叠技术

我们的目标是找到一个将字符串转换为数组索引的函数。只是为了说明这个想法，假设我们希望这个数组有 10 5 个元素的容量，让我们以字符串Java 语言为例。

4.1. 描述

让我们从将字符串的字符转换为数字开始。ASCII 很适合此操作：

现在，我们将刚刚获得的数字排列成一定大小的组。通常，我们根据数组的大小选择组大小值，即 10 5。由于我们将字符转换成的数字包含两到三位数字，不失一般性，我们可以将组大小设置为二：

下一步是将每个组中的数字连接起来，就好像它们是字符串一样，并求出它们的总和：

现在我们必须进行最后一步。让我们检查数字348933是否可以作为大小为 10 5的数组的索引。自然地，它超过了最大允许值*99999。*我们可以通过应用模运算符轻松克服这个问题，以便找到最终结果：

348933 % 10000 = 48933

4.2. 最后的评论

我们看到该算法不包含任何耗时的操作，因此速度非常快。**输入字符串的每个字符都会影响最终结果。**这个事实肯定有助于减少碰撞，但不能完全避免碰撞。

例如，如果我们想跳过折叠并将模运算符直接应用于 ASCII 转换的输入字符串（忽略溢出问题）

749711897321089711010311797103101 % 100000 = 3101

那么这样的哈希函数将为所有与我们的输入字符串具有相同最后两个字符的字符串产生相同的值：age、 page、 large等等。

从算法的描述中，我们很容易看出它并不是没有碰撞。例如，该算法为*Java language 和vaJa language *字符串生成相同的哈希值。

5. 其他技术

折叠技术很常见，但不是唯一的。有时，binning或mid-square技术也可能有用。

我们不使用字符串而是使用数字来说明他们的想法（假设我们已经以某种方式将字符串转换为数字）。我们不会讨论它们的优点和缺点，但是您可以在看到算法后形成意见。

5.1. Binning

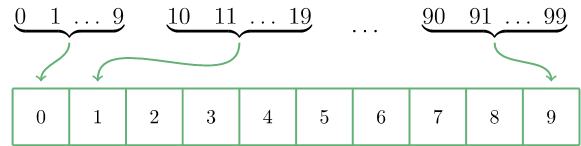
假设我们有 100 个整数，我们希望哈希函数将它们映射到一个包含 10 个元素的数组中。然后我们可以将这 100 个整数分成十组，这样前十个整数在第一个容器中结束，第二个十个整数在第二个容器中结束，依此类推：

5.2. Mid-Square

该算法由 John von Neumann 提出，它允许我们从给定数字开始生成伪随机数。

让我们用一个具体的例子来说明它。假设，我们有一个四位数的数字1111。根据算法，我们对其求平方，从而得到1234321。现在，我们从中间提取四位数字，例如2343。该算法允许我们重复这个过程，直到我们对结果满意为止。