Java中AVL树简介
1. 简介
在本教程中,我们将介绍 AVL 树,并研究用于插入、删除和搜索值的算法。
2. 什么是AVL树?
AVL 树以其发明者 Adelson-Velsky 和 Landis 命名,是一种自平衡二叉搜索树 (BST)。
自平衡树是一种二叉搜索树,它根据一些平衡规则来平衡插入和删除后的高度。
BST 的最坏情况时间复杂度是树高度的函数。具体来说,就是从树根到节点的最长路径。对于具有 N 个节点的 BST,假设每个节点只有零个或一个子节点。因此它的高度等于N,最坏情况下的搜索时间是O(N)。所以我们在 BST 中的主要目标是保持最大高度接近 log(N)。
节点 N 的平衡因子是height(right(N)) - height(left(N))。在 AVL 树中,节点的平衡因子只能是 1、0 或 -1 值之一。
让我们为我们的树定义一个Node对象:
public class Node {
int key;
int height;
Node left;
Node right;
...
}
接下来,让我们定义AVLTree:
public class AVLTree {
private Node root;
void updateHeight(Node n) {
n.height = 1 + Math.max(height(n.left), height(n.right));
}
int height(Node n) {
return n == null ? -1 : n.height;
}
int getBalance(Node n) {
return (n == null) ? 0 : height(n.right) - height(n.left);
}
...
}
3. 如何平衡 AVL 树?
AVL 树在插入或删除一个节点后检查其节点的平衡因子。如果节点的平衡因子大于 1 或小于 -1,则树会重新平衡自身。
重新平衡树有两种操作:
- 右旋转和
- 左旋转。
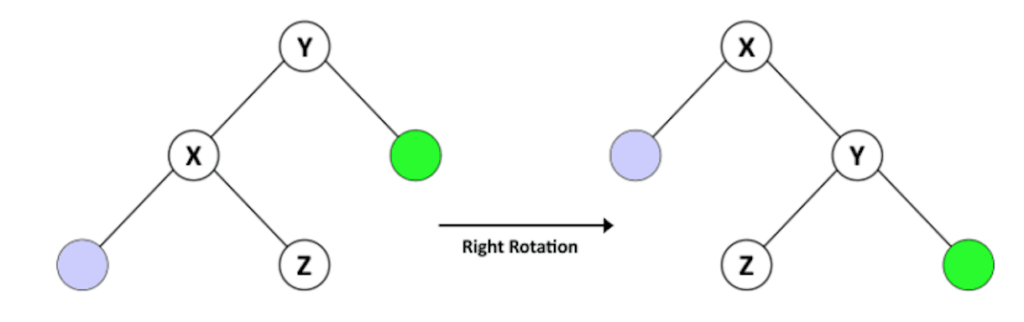
3.1. 右转
让我们从正确的旋转开始。
假设我们有一个名为 T1 的 BST,Y 为根节点,X 为 Y 的左孩子,Z 为 X 的右孩子。鉴于 BST 的特征,我们知道 X < Z < Y。
在 Y 向右旋转之后,我们有一个名为 T2 的树,其中 X 作为根,Y 作为 X 的右孩子,Z 作为 Y 的左孩子。T2 仍然是一个 BST,因为它保持 X < Z < Y .
让我们看看我们的AVLTree的正确旋转操作:
Node rotateRight(Node y) {
Node x = y.left;
Node z = x.right;
x.right = y;
y.left = z;
updateHeight(y);
updateHeight(x);
return x;
}
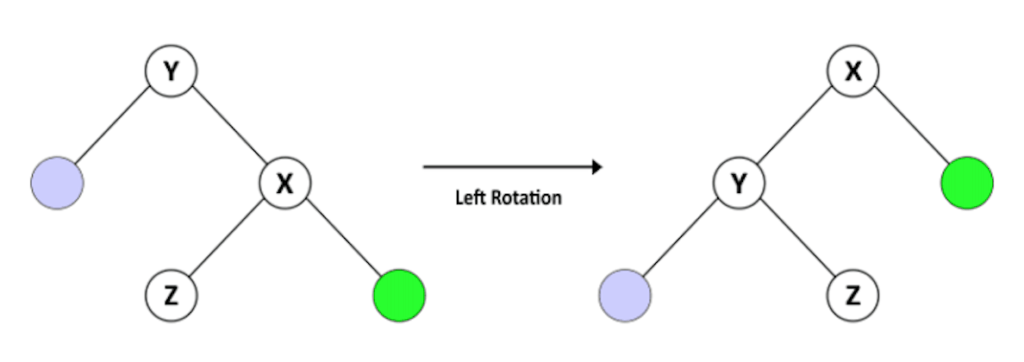
3.2. 左转操作
我们还有一个左旋转操作。
假设一个名为 T1 的 BST,以 Y 为根节点,X 为 Y 的右孩子,Z 为 X 的左孩子。鉴于此,我们知道 Y < Z < X。
在 Y 的左旋转之后,我们有一个名为 T2 的树,其中 X 作为根,Y 作为 X 的左孩子,Z 作为 Y 的右孩子。T2 仍然是一个 BST,因为它保持 Y < Z < X 的顺序.
让我们看一下我们的AVLTree的左旋转操作:
Node rotateLeft(Node y) {
Node x = y.right;
Node z = x.left;
x.left = y;
y.right = z;
updateHeight(y);
updateHeight(x);
return x;
}
3.3. 再平衡技术
我们可以在更复杂的组合中使用右旋转和左旋转操作来保持 AVL 树在其节点发生任何变化后保持平衡。在不平衡结构中,至少一个节点的平衡因子等于 2 或 -2。让我们看看如何在这些情况下平衡树。
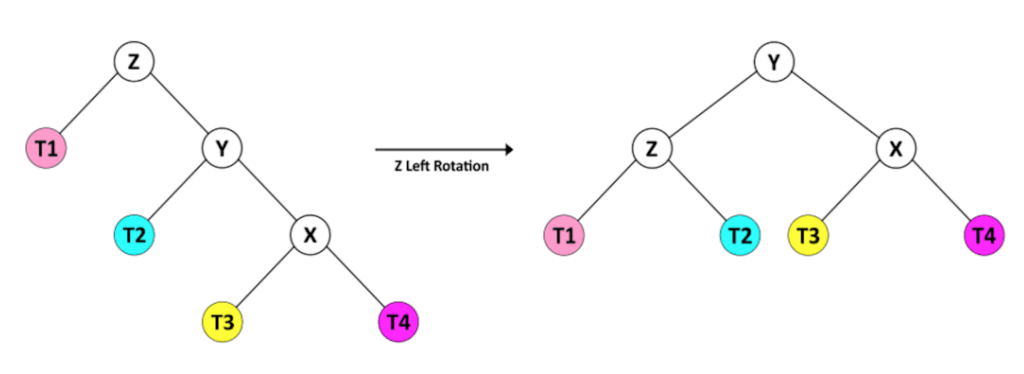
当节点 Z 的平衡因子为 2 时,以 Z 为根的子树处于这两种状态之一,将 Y 视为 Z 的右孩子。
对于第一种情况,Y (X) 的右孩子的高度大于左孩子的高度 (T2)。我们可以通过 Z 的左旋转轻松地重新平衡树。
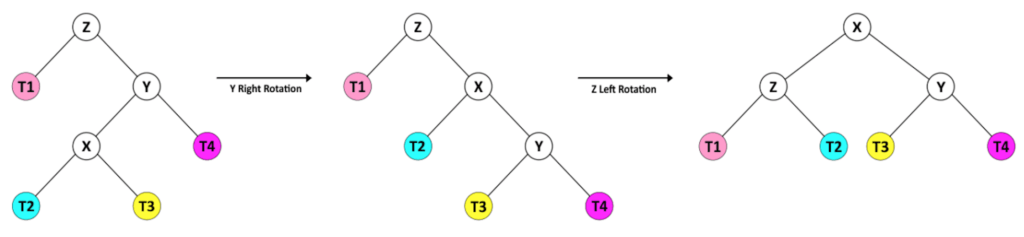
对于第二种情况,Y 的右孩子的高度(T4)小于左孩子的高度(X)。这种情况需要组合轮换操作。
在这种情况下,我们首先将 Y 向右旋转,因此树的形状与前一种情况相同。然后我们可以通过 Z 的左旋转来重新平衡树。
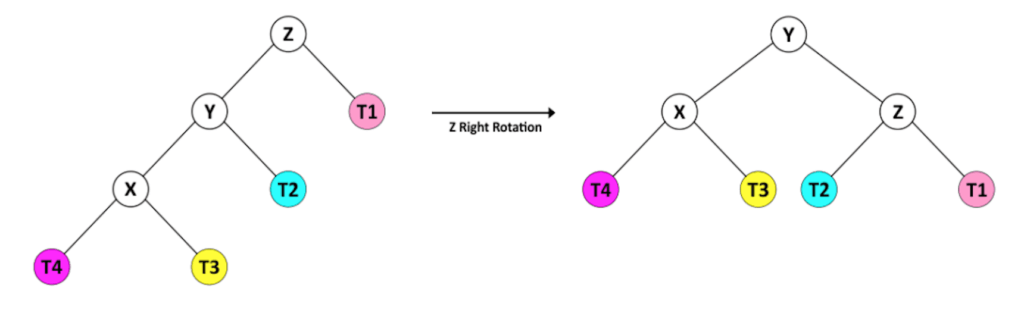
另外,当节点 Z 的平衡因子为 -2 时,其子树处于这两种状态之一,因此我们将 Z 视为根,将 Y 视为其左孩子。
Y 的左孩子的高度大于其右孩子的高度,所以我们用 Z 的右旋转来平衡树。
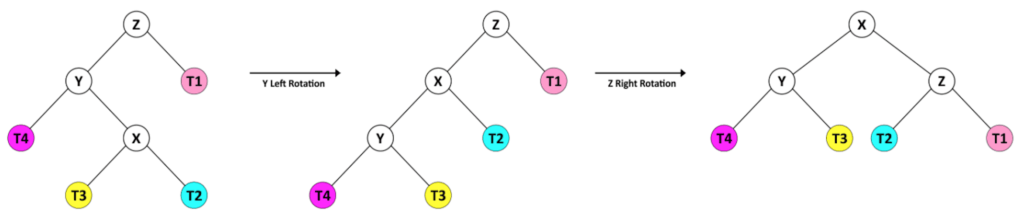
或者在第二种情况下,Y 的右孩子的高度大于其左孩子的高度。
因此,首先,我们将其转换为前一种形状,左旋转 Y,然后我们用右旋转 Z 平衡树。
让我们看一下AVLTree的重新平衡操作:
Node rebalance(Node z) {
updateHeight(z);
int balance = getBalance(z);
if (balance > 1) {
if (height(z.right.right) > height(z.right.left)) {
z = rotateLeft(z);
} else {
z.right = rotateRight(z.right);
z = rotateLeft(z);
}
} else if (balance < -1) {
if (height(z.left.left) > height(z.left.right))
z = rotateRight(z);
else {
z.left = rotateLeft(z.left);
z = rotateRight(z);
}
}
return z;
}
我们将在为从更改节点到根的路径中的所有节点插入或删除一个节点后使用重新平衡。
4. 插入一个节点
当我们要在树中插入一个键时,我们必须找到它的正确位置以通过 BST 规则。所以我们从根开始,将它的值与新的键进行比较。如果密钥更大,我们继续向右 - 否则,我们去左边的孩子。
一旦我们找到合适的父节点,然后我们将新键作为节点添加到左侧或右侧,具体取决于值。
插入节点后,我们有一个 BST,但它可能不是 AVL 树。因此,我们检查平衡因子并为从新节点到根的路径中的所有节点重新平衡 BST。
我们来看看插入操作:
Node insert(Node node, int key) {
if (node == null) {
return new Node(key);
} else if (node.key > key) {
node.left = insert(node.left, key);
} else if (node.key < key) {
node.right = insert(node.right, key);
} else {
throw new RuntimeException("duplicate Key!");
}
return rebalance(node);
}
重要的是要记住一个键在树中是唯一的——没有两个节点共享同一个键。
插入算法的时间复杂度是高度的函数。由于我们的树是平衡的,我们可以假设最坏情况下的时间复杂度为 O(log(N))。
5. 删除一个节点
要从树中删除一个键,我们首先必须在 BST 中找到它。
在我们找到节点(称为 Z)之后,我们必须引入新的候选节点作为它在树中的替换。如果 Z 是叶子,则候选为空。如果 Z 只有一个孩子,这个孩子就是候选者,但如果 Z 有两个孩子,则过程有点复杂。
假设 Z 的右孩子称为 Y。首先,我们找到 Y 的最左边的节点并将其称为 X。然后,我们将 Z 的新值设置为等于 X 的值,并继续从 Y 中删除 X。
最后,我们在最后调用 rebalance 方法来保持 BST 为 AVL 树。
这是我们的删除方法:
Node delete(Node node, int key) {
if (node == null) {
return node;
} else if (node.key > key) {
node.left = delete(node.left, key);
} else if (node.key < key) {
node.right = delete(node.right, key);
} else {
if (node.left == null || node.right == null) {
node = (node.left == null) ? node.right : node.left;
} else {
Node mostLeftChild = mostLeftChild(node.right);
node.key = mostLeftChild.key;
node.right = delete(node.right, node.key);
}
}
if (node != null) {
node = rebalance(node);
}
return node;
}
删除算法的时间复杂度是树的高度的函数。与插入方法类似,我们可以假设最坏情况下的时间复杂度为 O(log(N))。
6. 搜索节点
在 AVL 树中搜索节点与使用任何 BST 相同。
从树的根开始,将键与节点的值进行比较。如果键等于值,则返回节点。如果 key 更大,则从右孩子开始搜索,否则从左孩子继续搜索。
搜索的时间复杂度是高度的函数。我们可以假设最坏情况下的时间复杂度为 O(log(N))。
让我们看一下示例代码:
Node find(int key) {
Node current = root;
while (current != null) {
if (current.key == key) {
break;
}
current = current.key < key ? current.right : current.left;
}
return current;
}
 Coding Man
Coding Man